Параллелепипед
1. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны основанию.
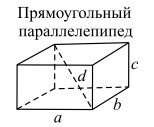
2. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным.
3. Свойства диагоналей прямоугольного параллелепипеда
а) диагонали прямоугольного параллелепипеда равны
б) квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер с общей вершиной).
4. Свойства граней и диагоналей параллелепипеда. Противоположные грани параллелепипеда равны и параллельны. Диагонали параллелепипеда пересекаются и делятся точкой пересечения пополам.
5. Диагональ AC1 параллелепипеда ABCDA1B1C1D1 проходит через точку пересечения медиан треугольника A1BD и делится ею в отношении 1 : 2, считая от точки A
6. Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Основные формулы
Далее V — объём тела, Sб и S — его боковая и полная поверхности
1. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны основанию.
2. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным.
3. Свойства диагоналей прямоугольного параллелепипеда
а) диагонали прямоугольного параллелепипеда равны
б) квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер с общей вершиной).
4. Свойства граней и диагоналей параллелепипеда. Противоположные грани параллелепипеда равны и параллельны. Диагонали параллелепипеда пересекаются и делятся точкой пересечения пополам.
5. Диагональ AC1 параллелепипеда ABCDA1B1C1D1 проходит через точку пересечения медиан треугольника A1BD и делится ею в отношении 1 : 2, считая от точки A
6. Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Основные формулы
Далее V — объём тела, Sб и S — его боковая и полная поверхности
| Чертежи | Обозначения | Формулы |
 | 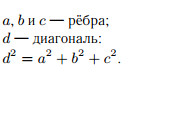 | 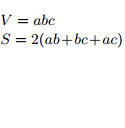 |
Комментариев нет:
Отправить комментарий