Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому. Давайте вспомним эти формулы и разберём примеры их применения.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):
c2 = a2 + b2
Площадь прямоугольного треугольника равна половине произведения его катетов:
S =ab/2.
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.
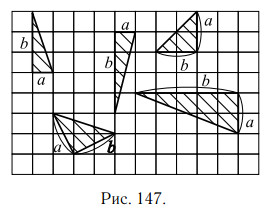
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.
Задачи с решениями
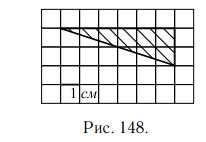
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем по клеточкам), поэтому площадь
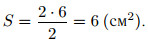
Ответ: 6
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
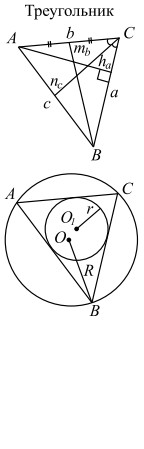 | a, b, c — стороны; A, B, C — противолежащие им углы; ha, hb, hc — высоты, проведённые к соответствующим сторонам; na, nb, nc — биссектрисы, проведённые к соответствующим сторонам; ba и bc — отрезки, на которые делится биссектрисой сторона b; ma, mb, mc — медианы, проведённые к соответствующим сторонам; 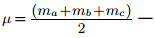 полусумма медиан; R — радиус описанной окружности; r — радиус вписанной окружности | 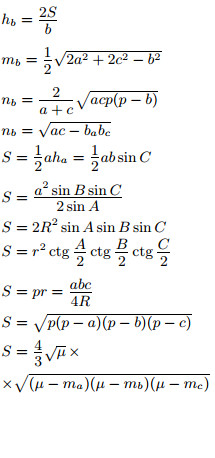 |
Прямоугольный треугольник
В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных на клетчатой бумаге или расположенных на координатной плоскости.Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому. Давайте вспомним эти формулы и разберём примеры их применения.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):
c2 = a2 + b2
Площадь прямоугольного треугольника равна половине произведения его катетов:
S =ab/2.
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.

Задачи с решениями
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.

Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем по клеточкам), поэтому площадь
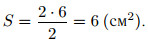
Ответ: 6
Комментариев нет:
Отправить комментарий