Круг и его элементы

Площади круга и сектора

Площадь круга равна произведению числа π на квадрат радиуса:

    S = πR2.



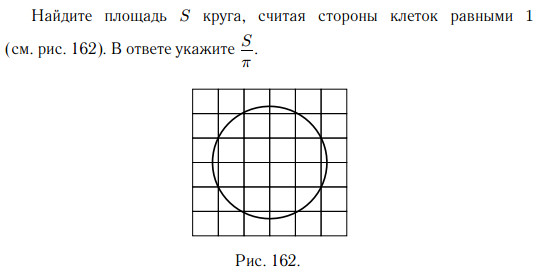
 Решение.
 Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)



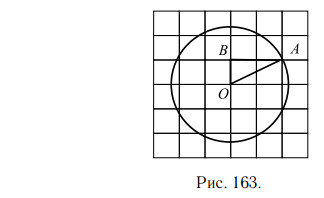
 Найдём гипотенузу по теореме Пифагора.

 Ответ: 5

 На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.



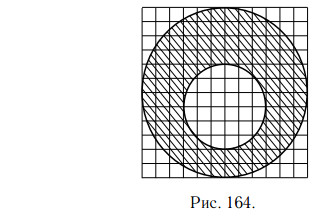
 Решение.
 Радиус R внутреннего круга — 3 клетки, его площадь равна πR2 = 3. Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна π · (2R)2 = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.
 Ответ: 9