Прямоугольник и Параллелограмм

Четырёхугольник

 Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
 Свойства и признаки параллелограмма
 1. Диагональ разбивает параллелограмм на два равных треугольника.
 2. Противоположные стороны параллелограмма попарно равны.
 3. Противоположные углы параллелограмма попарно равны.
 4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
 5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
 6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
 7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.

 Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.

 Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
 Свойства и признаки прямоугольника
 1. Диагонали прямоугольника равны.
 2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

 Квадрат. Квадратом называется прямоугольник, все стороны которого равны.

 Формулы площади четырёхугольника
 1. Площадь параллелограмма равна произведению основания на высоту
 2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
 3. Площадь прямоугольника равна произведению двух его соседних сторон.

 Основные формулы
 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи	Обозначения	Формулы
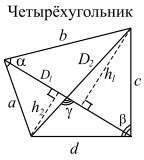	a, b, c, d — стороны;  D1, D2 — диагонали;  γ — угол между диагоналями;  h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника.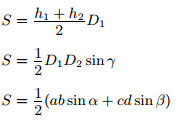
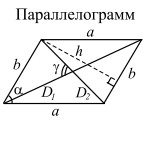	a, b — стороны; h — расстояние между сторонами b; α — угол параллелограмма;  D1, D2 — диагонали; γ — угол между диагоналями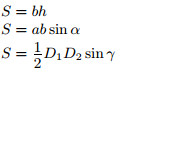

Площадь четырёхугольника

 Площадь прямоугольника равна произведению его смежных сторон:

    S = ab.

 На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b



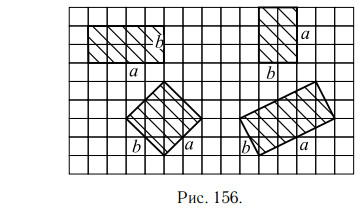
Задачи с решениями
 На клетчатой бумаге с клетками размером 1 см×1 см изображён прямоугольник (см. рис. 157). Найдите его площадь в квадратных сантиметрах.



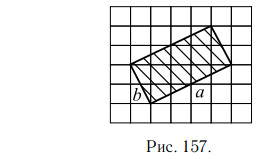
 Решение.
 1-й способ.
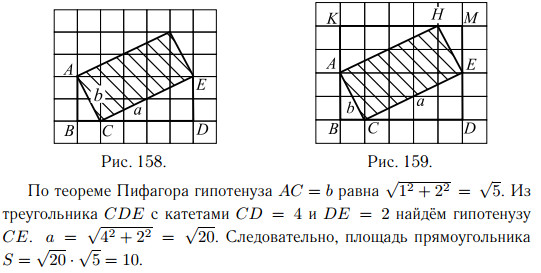
 Площадь прямоугольника равна произведению его смежных сторон a и b. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник ABC с катетами AB = 2 и BC = 1 и гипотенузой AC = b (см. рис. 158).


 Ответ: 10.

 2-й способ.
 Достроим прямоугольник ACEH до прямоугольника BKMD (см. рис. 159). Чтобы найти площадь ACEH, нужно из площади прямоугольника BKMD вычесть площади прямоугольных треугольников AKH, HME, EDC и ABC.
 Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников (AKH и EDC) равна 4, а площадь каждого из двух маленьких треугольников (HME и ABC) равна 1. Площадь прямоугольника BKMD равна 4 · 5 = 20. Следовательно, площадь искомого прямоугольника будет равна 20 − 1 − 1 − 4 − 4 = 10.
 Ответ: 10.
 Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.