Рассмотрим прямоугольную систему координат Oxy (см. рис. 207). Длина отрезка AB, для которого известны координаты его концов A(xA; yA) и B(xB; yB), определяется по формуле
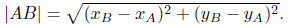
Координаты середины отрезка вычисляются по формулам:

Если точки A и B симметричны относительно оси Ox (оси абсцисс), то их ординаты противоположны (см. рис. 208), а абсциссы равны: A(x; y), B(x; −y).
Если точки A и C симметричны относительно оси Oy, то их абсциссы противоположны, а ординаты равны: A(x; y), C(−x; y).
Если точки A и D симметричны относительно начала координат, то их координаты противоположны: A(x; y), D(−x; −y).
Координаты и векторы в пространстве
1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.


4. Любой вектор можно единственным образом разложить по трём некомпланарным векторам.

9. Координаты середины отрезка равны средним арифметическим координат его концов.
10. Свойства скалярного произведения векторов:



Решение.
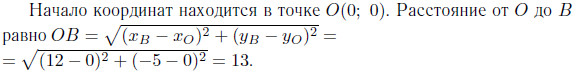
Ответ: 13.
Найдите абсциссу точки, симметричной точке A(2; 5) относительно оси Oy (см. рис. 210).

Решение.
Точке A симметрична точка B(−2; 5) (см. рис. 211). Абсцисса точки B равна −2
Ответ: -2.
Найдите ординату середины отрезка, соединяющего точки A(−4; 6) и B(2; 4) (см. рис. 212).

Решение.

Ответ: 5.
Точки A(−1; −2), B(4; −1), C(6; 5) и D являются вершинами параллелограмма. Найдите абсциссу точки P пересечения его диагоналей (см. рис. 213).

Решение.

Ответ: 2,5
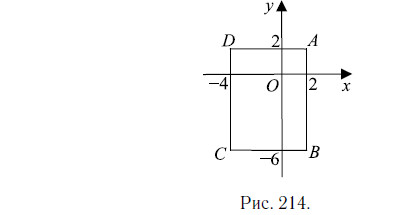
Найдите ординату центра окружности (см. рис. 214), описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (2; 2), (2; −6), (−4; −6), (−4; 2)
Решение.

Ответ: -2
Точки O(0; 0), B(8; 2), C(0; 8) являются вершинами параллелограмма (см. рис. 215). Найдите ординату точки M

Решение.
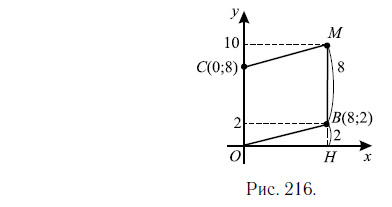
Ордината — это координата по оси Oy. Она равна длине отрезка HM (см. рис. 216). HB = 2, так как ордината B равна 2. Поскольку противоположные стороны параллелограмма равны, то OC = BM = 8. Тогда HM = 2 + 8 = 10
Ответ: 10
Прямая a проходит через точки с координатами (0; 2) и (−4; 0). Прямая b проходит через точку с координатами (0; −4) и параллельна прямой a (см. рис. 217). Найдите абсциссу точки пересечения прямой b с осью Ox.
Решение.
1-й способ.
Нарисуем картинку на клетчатой бумаге (см. рис. 218).

Абсцисса точки пересечения прямой b с осью Ox равна длине отрезка OA. Так как прямые параллельны, углы HCO и ABK равны, достроим 2 треугольника BKT и TMA, равных треугольнику HCO.
OA = BK + TM = 4 + 4 = 8.
Ответ: 8.
2-й способ.
Треугольники CHO и BOA подобны по трём углам (см. рис. 219), значит, их стороны пропорциональны. OB : OH = OA : OC, тогда 4 : 2 = OA : 4. OA = 8.

Ответ: 8
Найдите угловой коэффициент прямой, проходящей через точки с координатами (12; 0) и (0; 12) (см. рис. 220).

Решение.
1-й способ.
Угловой коэффициент прямой равен тангенсу угла, который прямая образует с положительным направлением оси Ox (там, где на оси стрелочка). В нашей задаче это угол a (см. рис. 221).

Ответ: -1
2-й способ.

Ответ: -1
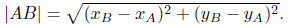
Координаты середины отрезка вычисляются по формулам:

Если точки A и B симметричны относительно оси Ox (оси абсцисс), то их ординаты противоположны (см. рис. 208), а абсциссы равны: A(x; y), B(x; −y).
Если точки A и C симметричны относительно оси Oy, то их абсциссы противоположны, а ординаты равны: A(x; y), C(−x; y).
Если точки A и D симметричны относительно начала координат, то их координаты противоположны: A(x; y), D(−x; −y).
Координаты и векторы в пространстве
1. Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.


4. Любой вектор можно единственным образом разложить по трём некомпланарным векторам.

9. Координаты середины отрезка равны средним арифметическим координат его концов.
10. Свойства скалярного произведения векторов:



Задачи с решениями
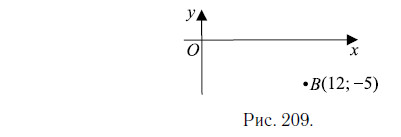
Найдите расстояние от точки B с координатами (12; −5) до начала координат (см. рис. 209)
Решение.
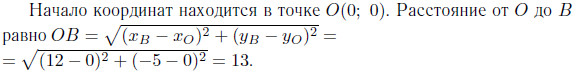
Ответ: 13.
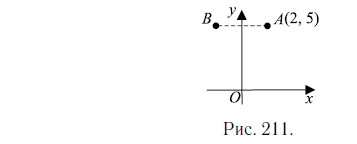
Найдите абсциссу точки, симметричной точке A(2; 5) относительно оси Oy (см. рис. 210).

Решение.
Точке A симметрична точка B(−2; 5) (см. рис. 211). Абсцисса точки B равна −2

Ответ: -2.
Найдите ординату середины отрезка, соединяющего точки A(−4; 6) и B(2; 4) (см. рис. 212).

Решение.

Ответ: 5.
Точки A(−1; −2), B(4; −1), C(6; 5) и D являются вершинами параллелограмма. Найдите абсциссу точки P пересечения его диагоналей (см. рис. 213).

Решение.

Ответ: 2,5
Найдите ординату центра окружности (см. рис. 214), описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (2; 2), (2; −6), (−4; −6), (−4; 2)

Решение.

Ответ: -2
Точки O(0; 0), B(8; 2), C(0; 8) являются вершинами параллелограмма (см. рис. 215). Найдите ординату точки M

Решение.
Ордината — это координата по оси Oy. Она равна длине отрезка HM (см. рис. 216). HB = 2, так как ордината B равна 2. Поскольку противоположные стороны параллелограмма равны, то OC = BM = 8. Тогда HM = 2 + 8 = 10

Ответ: 10
Прямая a проходит через точки с координатами (0; 2) и (−4; 0). Прямая b проходит через точку с координатами (0; −4) и параллельна прямой a (см. рис. 217). Найдите абсциссу точки пересечения прямой b с осью Ox.
Решение.
1-й способ.
Нарисуем картинку на клетчатой бумаге (см. рис. 218).

Абсцисса точки пересечения прямой b с осью Ox равна длине отрезка OA. Так как прямые параллельны, углы HCO и ABK равны, достроим 2 треугольника BKT и TMA, равных треугольнику HCO.
OA = BK + TM = 4 + 4 = 8.
Ответ: 8.
2-й способ.
Треугольники CHO и BOA подобны по трём углам (см. рис. 219), значит, их стороны пропорциональны. OB : OH = OA : OC, тогда 4 : 2 = OA : 4. OA = 8.

Ответ: 8
Найдите угловой коэффициент прямой, проходящей через точки с координатами (12; 0) и (0; 12) (см. рис. 220).

Решение.
1-й способ.
Угловой коэффициент прямой равен тангенсу угла, который прямая образует с положительным направлением оси Ox (там, где на оси стрелочка). В нашей задаче это угол a (см. рис. 221).

Ответ: -1
2-й способ.

Ответ: -1
Комментариев нет:
Отправить комментарий