Задачи с решениями
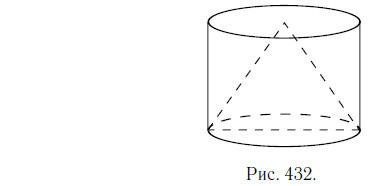
Цилиндр и конус имеют общее основание и общую высоту (см. рис. 432). Вычислите объём цилиндра, если объём конуса равен 16.
Решение

Ответ: 48.
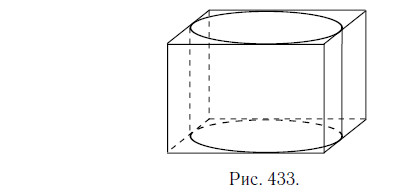
Прямоугольный параллелепипед описан около цилиндра (см. рис. 433), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.
Решение
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть 2 · 5 = 10. Площадь основания параллелепипеда равна 10 · 10 = 100. Высоту h параллелепипеда находим из формулы объёма параллелепипеда: 100h = 600; h = 6. Найденная высота параллелепипеда одновременно является и высотой цилиндра. Ответ: 6.
Объём куба равен 30 (см. рис. 434). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение

Ответ: 5.
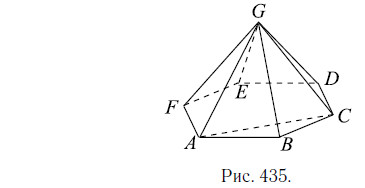
Объём правильной шестиугольной пирамиды GABCDEF равен 60 (см. рис. 435). Найдите объём треугольной пирамиды GABC.
Решение
Обозначим сторону шестиугольника в основании пирамиды через r. Правильный шестиугольник можно разбить на 6 правильных треугольников (как в задаче 12), поэтому площадь шестиугольника равна
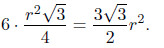
Найдём площадь треугольника ABC
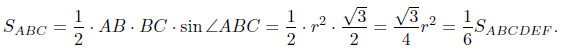
Таким образом, площадь основания пирамиды GABC в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
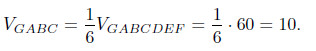
Ответ: 10.
Цилиндр и конус имеют общее основание и общую высоту (см. рис. 432). Вычислите объём цилиндра, если объём конуса равен 16.
Решение


Ответ: 48.
Прямоугольный параллелепипед описан около цилиндра (см. рис. 433), радиус основания которого равен 5. Объём параллелепипеда равен 600. Найдите высоту цилиндра.

Решение
Каждая сторона прямоугольника в основании параллелепипеда равна диаметру цилиндра, то есть 2 · 5 = 10. Площадь основания параллелепипеда равна 10 · 10 = 100. Высоту h параллелепипеда находим из формулы объёма параллелепипеда: 100h = 600; h = 6. Найденная высота параллелепипеда одновременно является и высотой цилиндра. Ответ: 6.
Объём куба равен 30 (см. рис. 434). Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение

Ответ: 5.
Объём правильной шестиугольной пирамиды GABCDEF равен 60 (см. рис. 435). Найдите объём треугольной пирамиды GABC.

Решение
Обозначим сторону шестиугольника в основании пирамиды через r. Правильный шестиугольник можно разбить на 6 правильных треугольников (как в задаче 12), поэтому площадь шестиугольника равна
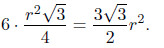
Найдём площадь треугольника ABC
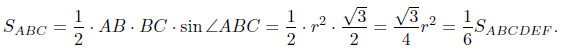
Таким образом, площадь основания пирамиды GABC в 6 раз меньше площади основания шестиугольной пирамиды, а их высоты совпадают. Поэтому объёмы этих пирамид находятся в том же соотношении, что и площади их оснований.
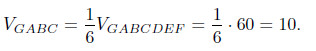
Ответ: 10.
Комментариев нет:
Отправить комментарий