Пирамида
1. Если боковые грани треугольной пирамиды образуют равные двугранные углы с плоскостью основания, то высота пирамиды проходит либо через центр вписанной окружности, либо через центр одной из вневписанных окружностей основания.2. Если все боковые рёбра пирамиды образуют с основанием равные углы или если все боковые рёбра равны, то высота пирамиды проходит через центр окружности, описанной около основания.
3. Теорема о медианах тетраэдра. Медианы тетраэдра (отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противолежащих граней) пересекаются в одной точке и делятся ею в отношении 3 : 1, считая от вершины.
4. Если пересечь пирамиду плоскостью, параллельной основанию, то в сечении образуется многоугольник, подобный основанию.
5. В пирамиде и в конусе площади сечений, параллельных основанию, относятся как квадраты их расстояний до вершины.
6. Объём пирамиды равен трети произведения площади основания на высоту.
7. Пирамиды с равными высотами и равновеликими основаниями равновелики.
8. Плоскость, проходящая через вершину пирамиды и прямую, лежащую в основании, делит объём пирамиды в том же отношении, в котором прямая делит площадь основания.
9. Если точки A1, B1 и C1 лежат на боковых рёбрах DA, DB и DC соответственно треугольной пирамиды ABCD или на их продолжениях, то объём пирамиды A1B1C1D1 относится к объёму пирамиды ABCD как произведение отношений
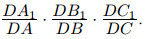
Основные формулы
Далее V — объём тела, Sб и S — его боковая и полная поверхности
| Чертежи | Обозначения | Формулы |
 | F — площадь основания; h — высота; P — периметр основания; a — апофема (высота боковой грани правильной пирамиды). |  |
 | F, f — площади оснований; h — высота (расстояние между основаниями); A, a — две соответственные стороны оснований. | 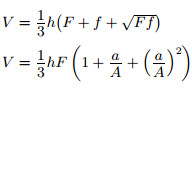 |
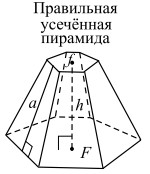 | F, f — площади оснований; P, p — периметры оснований; h — высота; a — апофема (высота боковой грани). | 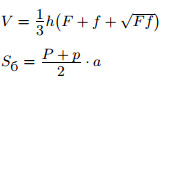 |
Правильная пирамида
1. Если AB CD — правильная треугольная пирамида с вершиной D, высотой DM и стороной основания a, а A1, B1 и C1 — середины сторон BC, AC и AB соответственно, то
а) ∠ D A M = ∠ D B M = ∠ D C M — угол бокового ребра с плоскостью основания;
б) ∠ D A1 M = ∠ D B1M = ∠ D C1M — линейный угол двугранного угла боковой грани с плоскостью основания;
в) ∠A F B (где F — основание перпендикуляра, опущенного из вершины A основания на боковое ребро DC) — линейный угол между боковыми гранями пирамиды;
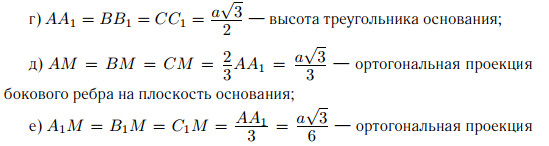
ж) C1F — общий перпендикуляр противоположных рёбер AB и CD
2. Противоположные рёбра правильной треугольной пирамиды попарно перпендикулярны.
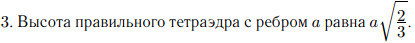
4. Если PABCD — правильная четырёхугольная пирамида с вершиной P, высотой PM и стороной основания a, а A1, B1, C1 и D1 — середины сторон AB, BC, CD и AD соответственно, то
а) ∠ P A M = ∠ P B M = ∠ P C M = ∠ P D M — угол бокового ребра с плоскостью основания
б) ∠ P A1M = ∠ P B1M = ∠ P C1M = ∠ P D1M — линейный угол двугранного угла боковой грани с плоскостью основания;
в) ∠ B F D (где F — основание перпендикуляра, опущенного из вершины B основания на боковое ребро AP) — линейный угол между соседними боковыми гранями пирамиды;
г) ∠ A1P C1 = ∠ B1P D1 — линейный угол двугранного угла между противоположными боковыми гранями;
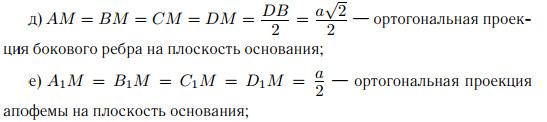
ж) F M — общий перпендикуляр диагонали B D основания и скрещивающегося с ней бокового ребра AP
5. Боковое ребро правильной четырёхугольной пирамиды перпендикулярно скрещивающейся с ним диагонали основания
6. Площадь боковой поверхности правильной пирамиды равна площади её основания, делённой на косинус угла боковой грани с плоскостью основания.
Тетраэдр.

12. A. Объём тетраэдра равен трети произведения его полной поверхности на радиус вписанной сферы
Правильный тетраэдр. Пусть a — ребро правильного тетраэдра, а R и r — радиусы описанной и вписанной сфер, V — объём тетраэдра. Тогда
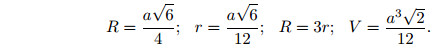
Комментариев нет:
Отправить комментарий